RubNNet4MD:
Ruhr-Universität Bochum Neural Networks for Molecular Dynamics Simulations
RubNNet4MD is a program package developed at the Center for Theoretical Chemistry of the Ruhr-Universität Bochum that implements high-dimensional neural network techniques for use in computational physics and chemistry, in particular molecular dynamics and Monte Carlo simulations with a focus on applications in molecular sciences. High-dimensional neural network potentials (HD-NNP) have been pioneered by Behler and Parrinello [1]. The fundamental methodology and its subsequent advances have been repeatedly reviewed by Behler [2, 3, 4]. The main idea is to use artificial neural networks (NNs), specifically fully connected feed-forward NNs, trained against a set of reference data to represent the potential energy surface (PES) and interatomic forces of various finite molecular and extended condensed matter systems.
Within the HD-NNP framework, the total energy of the system is represented as a sum of atomic contributions which are the output of atomic NNs. These atomic NNs take as input a precise fingerprint of the chemical environment around the considered atom described by "symmetry functions" [5] that ensure a description of the local environment which is fully invariant to translation and rotation as well as to permutations of all atoms of the same type. The typical architecture of these HD-NNPs is schematically depicted in Figure 1. Interatomic forces can be obtained by differentiating the neural network PES, which can be done analytically. Reference force information can also be used during the training of the NNPs in conjunction with the reference energies.
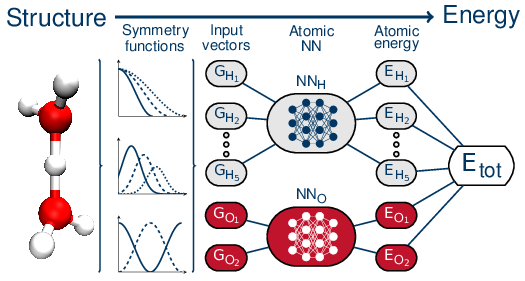
Figure 1. A schematic depiction of the architecture used in high-dimensional neural networks. Figure from Reference [6].
RubNNet4MD is a Fortran program to easily and efficiently train such NNs for the description of molecular and condensed systems. The program also provides a standalone library for the evaluation of these NNs that can be used in separate molecular simulation packages, notably including CP2K. Various aspects of RubNNet4MD are influenced by the RuNNer program [7], which was the first general implementation of HD-NNPs created by Jörg Behler while he was the head of an independent Emmy Noether Group here at the Center for Theoretical Chemistry at RUB.
So far, we used such HD-NNPs since 2018 to accurately represent global potential energy surfaces in full dimensionality (NN-PES) of molecular complexes and clusters at essentially converged Coupled Cluster electronic structure accuracy for use in molecular simulation with classical and quantum nuclei [8, 9, 10, 11], see Figures 2 and 3.
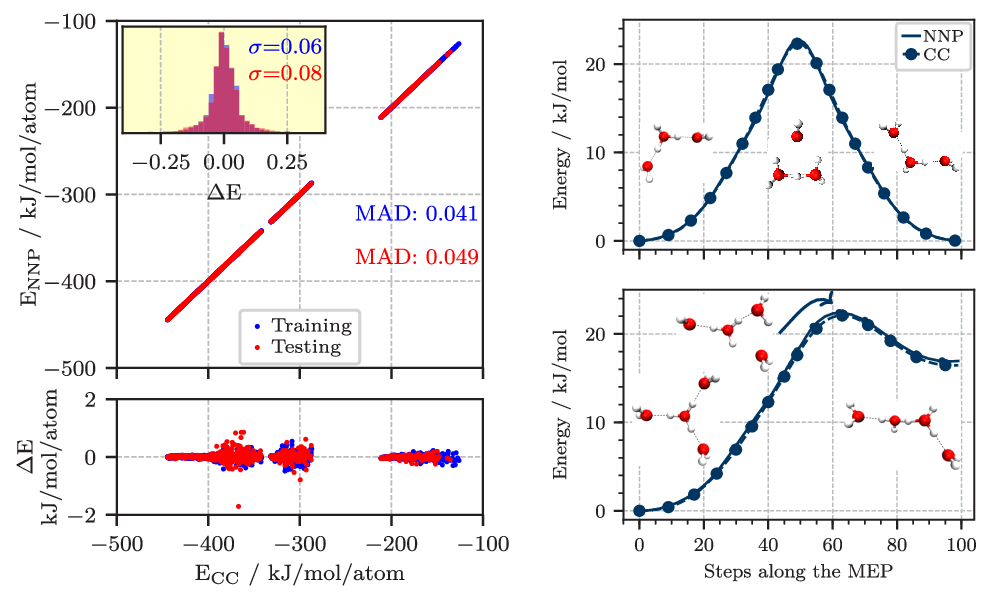
Figure 2. Left: Correlation of the energy per atom from explicit CCSD(T*)-F12a/aug-cc-pVTZ calculations (CC) and the NNP predictions for the final reference data set describing protonated water clusters from the hydronium cation, H3O+ up to the tetramer, H9O4+. The mean absolute difference (MAD) for the training and test set are given in blue and red, respectively. The lower panel shows the errors, while the inset in the upper panel shows the histograms of these errors including the corresponding standard deviations (σ) in the respective color. Right: Potential energy profiles of the H7O3+ (top) and H9O4+ (bottom) clusters along selected minimum energy paths (MEP) obtained using the zero temperature string method on the neural network potential (NNP). The coupled cluster (CC) reference was obtained by recomputing the energies along the NNP paths at representative points and is marked with circles. All energies are shown relative to the respective equilibrium structures. Figures from Reference [6].
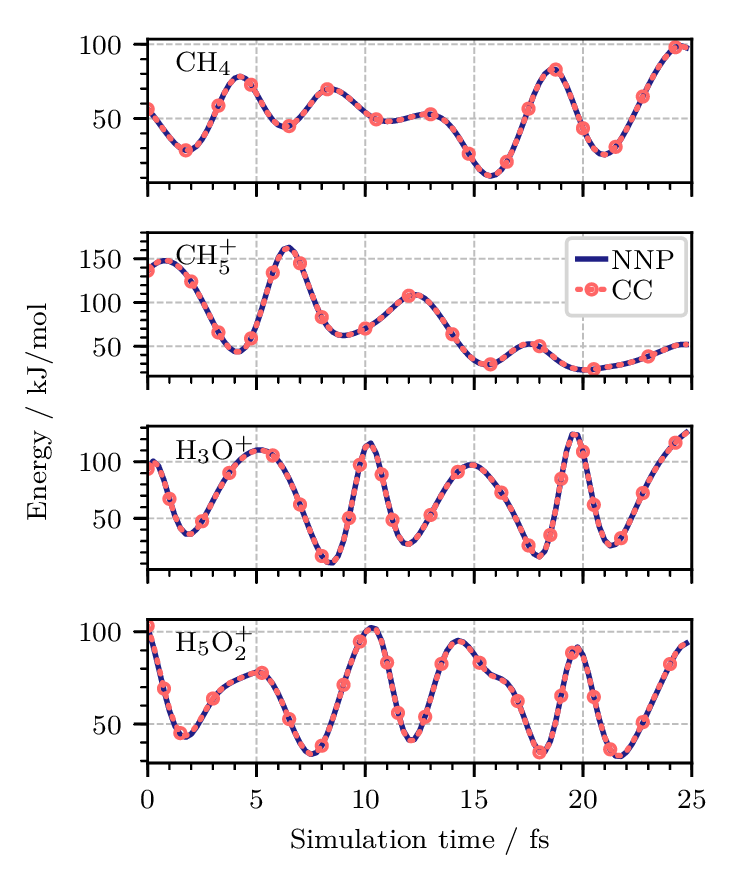
Figure 3. Potential energy along one replica of quantum PIMD trajectories of (from top to bottom) the methane molecule, CH4, the protonated methane complex, CH5+, the hydronium cation, H3O+, and the Zundel cation, H5O2+, at 1.67 K using neural network potentials (NNPs). The coupled cluster CCSD(T*)-F12a/AVTZ reference data (CC) were obtained by recomputing the energies at each step of the NNP trajectories and are shown as red dotted lines. All energies are reported relative to the equilibrium structures of the respective global minima. Figure from Reference [10].
A similar technique has been used successfully to describe the weak van der Waals interactions of helium with molecular species, see Figure 4.
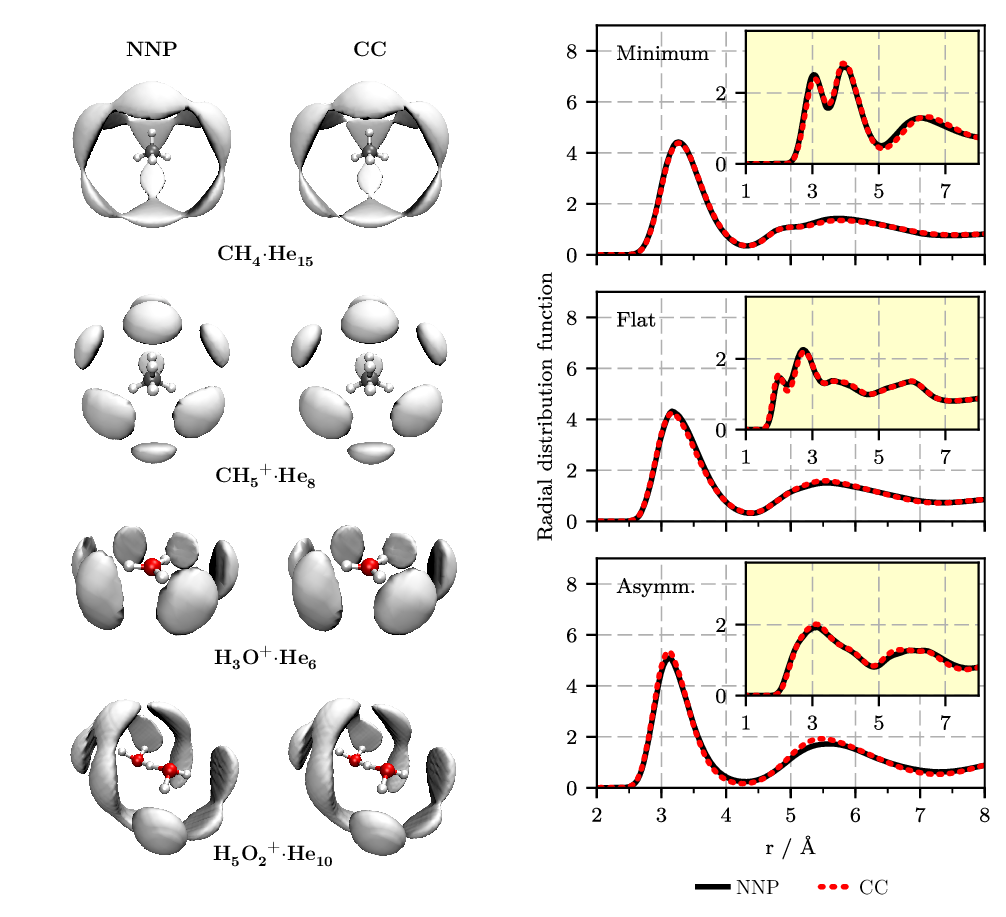
Figure 4. Left: Spatial distribution functions (SDFs) of helium atoms around a fixed molecular impurity, as sampled from PIMC simulations at 1.67 K. The solute ... helium interaction energies are interpolated from pre-computed values on a grid using either the neural network potential (NNP: left column) or single-point counterpoise-corrected coupled cluster calculations, CCSD(T*)-F12a/AVTZcp (CC: right column). Right: Radial distribution functions for oxygen-helium (main) and hydrogen-helium (inset) for frozen H5O2+ configurations in bulk helium in a selected orientation close to the minimum energy structure (“minimum,” top), in a flat orientation (“flat,” middle), and in an asymmetric proton transfer situation (“asymm,” bottom) centered in a truncated octahedron periodic supercell hosting in addition 88 He atoms. Figures from References [9 , 10].
Our approach to parameterize such highly accurate interactions potentials has been generalized to describe solvation (or “tagging”) of solute species by para-hydrogen, pH2, molecules. This has been established by performing the adiabatic hindered rotor (AHR) average that considers the impact of nuclear spin statistics on the allowed rotational states at the level of an interim all-atom neural network interaction potential, see Figure 5. The quality of these AHR-averaged NNPs of converged CCSD(T) quality is very similar to that demonstrated earlier for helium atom interactions (see Figure 4).
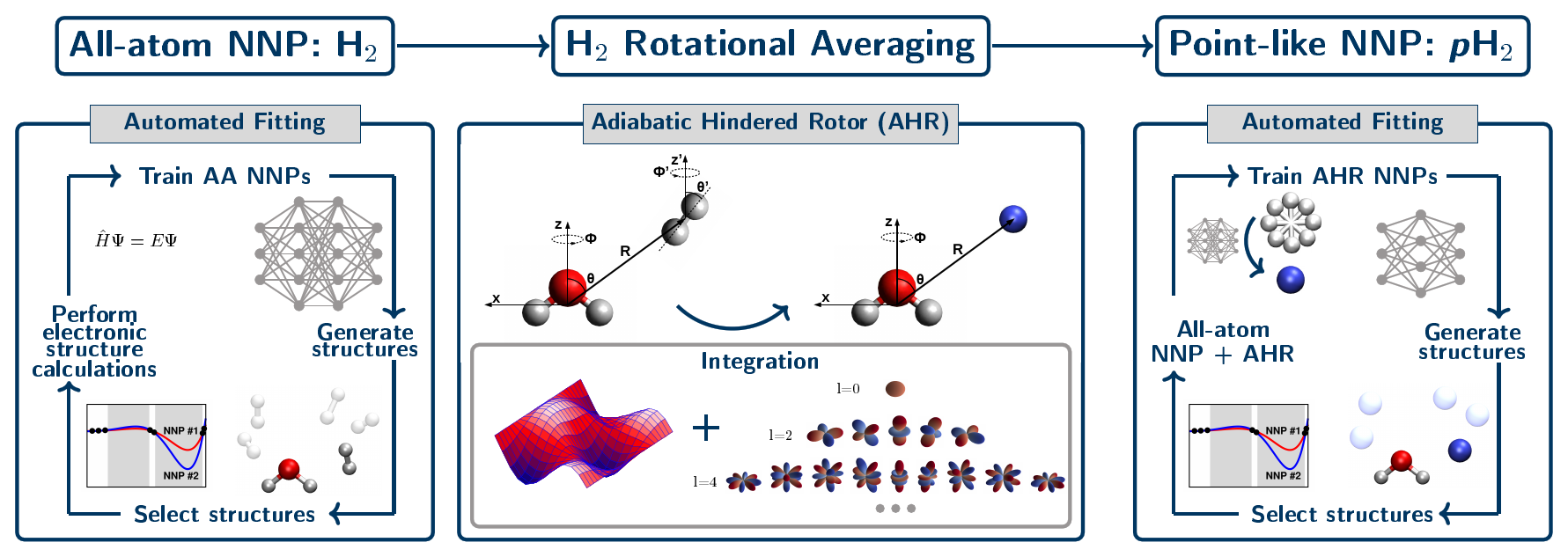
Figure 5. Schematic representation of our data-driven three-step development process for generating all-atom H2 and single-site AHR-averaged pH2 neural network interaction potentials. The left panel shows the generation of the interim all-atom interaction NNP via an automated active learning procedure where the diatomic nature of the H2 molecule is explicitly considered. Then, that final all-atom NNP is used to perform the adiabatic hindered rotor (AHR) averaging (middle panel). In this step we reduce the dimensionality of the pH2 molecule from all-atom to a point-like particle, while imposing the required nuclear spin statistics for pH2 by only including the even rotational energy levels in the orientational average. Finally, the AHR-averaged NNP is generated, where pH2 is a point-like and thus effective spherical particle (right panel). Figure from Reference [12].
The HD-NNP framework can also be used to parameterize neutral network dipole moment surfaces (NN-DMS) in addition to the corresponding potential energy surfaces (NN-PES), thus providing the total dipole moment vector of the system at each configuration [13]. We have introduced such a technique that strictly conserves the total charge of the system by construction and is based on CCSD(T) quality dipole moments, see Figure 6. Using this NN-DMS [13] together with the NN-PES [6], quasi-exact infrared spectra can be computed from quantum dynamics at converged CCSD(T) accuracy as demonstrated for the protonated water dimer or Zundel complex [14].
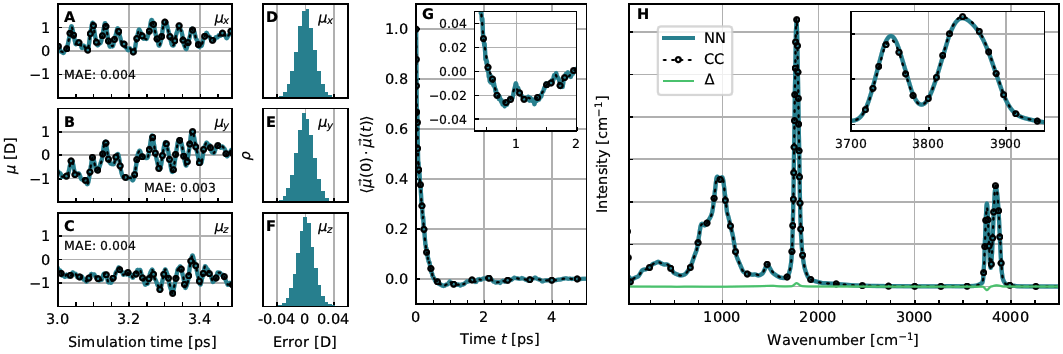
Figure 6. Performance of the NN-DMS for the bare Zundel complex, H5O2+. A to C: Short excerpts from classical MD trajectories at 100 K comparing the dipole moments from explicit CCSD(T) calculations to those from the NN-DMS separated into their x-, y- and z-components; the corresponding MAE is provided in the respective panels. D to F: Corresponding error distributions over all 60 NVE trajectories generated to compute the IR spectrum in panel H. G: Dipole autocorrelation function from NN and CC dipole moments as obtained from DF-CCSD(T*)-F12a/aug-cc-pVDZ electronic structure reference calculations. H: IR spectrum of the protonated water dimer at 100 K computed from NN and CC dipole moments from the same set of trajectories. The magnified peak in the inset visualizes some very small difference in peak intensity whereas the Δ line quantifies the spectral differences as a function of frequency. Figure from Reference [13].
A major breakthrough was the transfer of CCSD(T) accuracy from finite systems in the gas phase to condensed phase systems using HD-NNPs as demonstrated for bulk liquid water [15], based on using RubNNet4MD combined with our HD-NNP interface to the open-source CP2K molecular dynamics simulation package. Excellent agreement with experimental structural and dynamical properties has been achieved. The method is general and, thus, is called coupled cluster molecular dynamics, CCMD. The fundamental ideas and the conceptual details of our CCMD approach are exposed in the top and bottom panels of Figure 7, respectively.
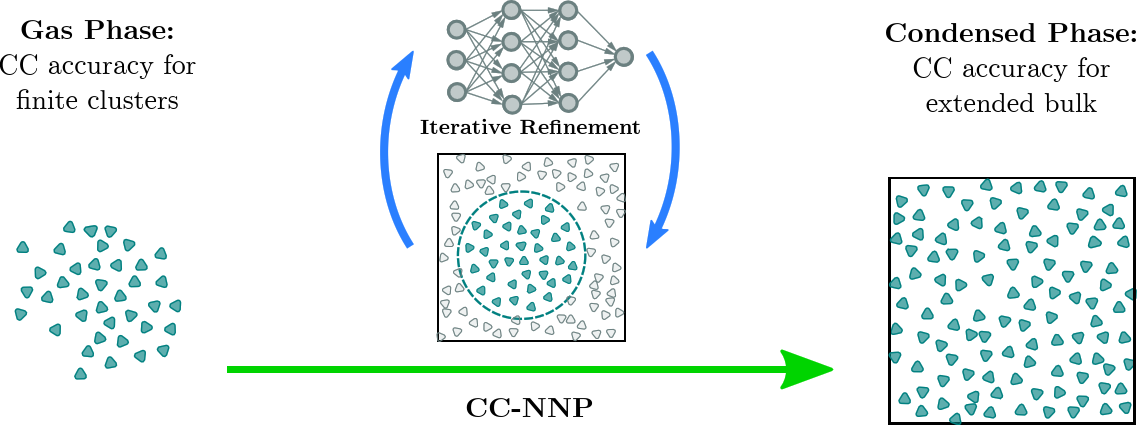
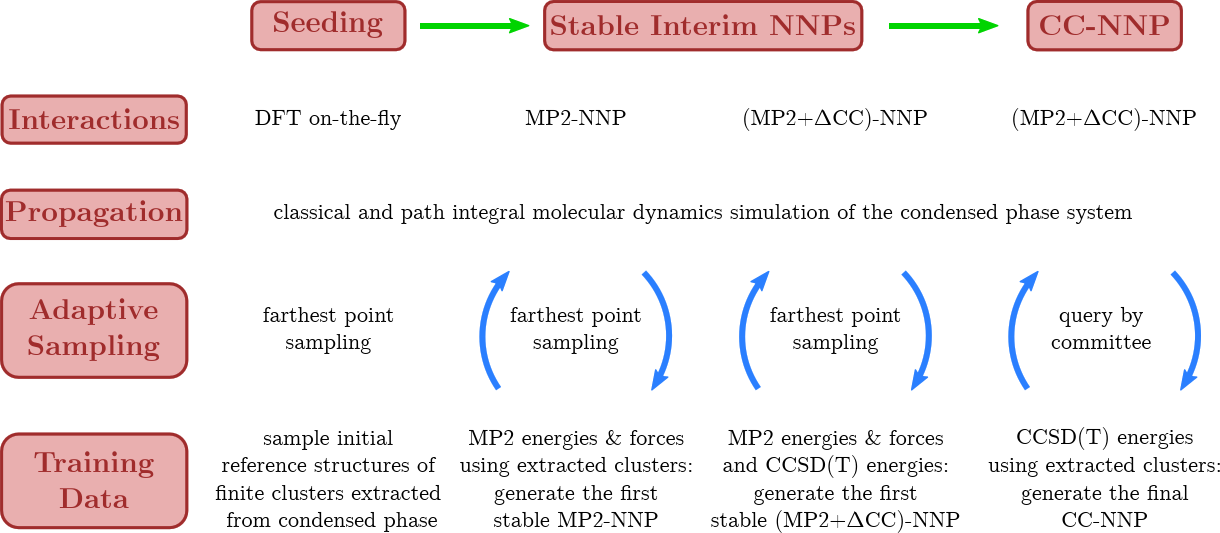
Figure 7. Schematic visualization of our generic approach to CCMD simulations of general condensed phase systems at CCSD(T) accuracy based on HD-NNPs. Top: General concept to transfer CCSD(T) accuracy (blue species) from isolated gas phase systems (left) to extended condensed phase systems (right) using HD-NNPs trained on cluster reference data that have been adaptively sampled from condensed phase simulations (center). Bottom: Generation of the final HD-NNP at CCSD(T) accuracy for CCMD simulations based on sampling of initial reference structures from DFT-based on-the-fly simulations (Seeding: left) followed by the generation of the interim MP2-HDNNP and its improvement using additional CCSD(T) energies ΔCC based on reference structures sampled from the respective interim-HDNNP simulations (Stable Interim NNPs: center) and the subsequent refinement yielding the final CCSD(T)-HDNNP (CC-NNP: right) all based on active learning techniques. Figure from the Supplemental Material of Reference [15].
Code Availability
The RUBNNet4MD package can be accessed via https://doi.org/10.17877/RESOLV-2025-MDN6B2J4.
References
[1] J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett. 98, 146401 (2007)
[2] J. Behler, Representing potential energy surfaces by high-dimensional neural network potentials, J. Phys.: Condens. Matter 26, 183001 (2014)
[3] J. Behler, Constructing high‐dimensional neural network potentials: A tutorial review, Int. J. Quantum Chem. 115, 1032 (2015)
[4] J. Behler, First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems, Angew. Chem. Int. Ed 56, 12828 (2017) ; J. Behler, Four Generations of High-Dimensional Neural Network Potentials, Chem. Rev. 121, 10037 (2021)
[5] J. Behler, Atom-centered symmetry functions for constructing high-dimensional neural network potentials, J. Chem. Phys. 134, 074106 (2011)
[6] C. Schran, J. Behler, and D. Marx, Automated Fitting of Neural Network Potentials at Coupled Cluster Accuracy: Protonated Water Clusters as Testing Ground, J. Chem. Theory Comput. 16, 88 (2020)
[7] J. Behler, RuNNer: A program for constructing high-dimensional neural network potentials; Georg-August-Universität Göttingen, Germany, https://www.uni-goettingen.de/de/560580.html
[8] C. Schran, F. Brieuc, and D. Marx, Converged Colored Noise Path Integral Molecular Dynamics Study of the Zundel Cation Down to Ultralow Temperatures at Coupled Cluster Accuracy, J. Chem. Theory Comput. 10, 5068 (2018)
[9] C. Schran, F. Uhl, J. Behler, and D. Marx, High-dimensional neural network potentials for solvation: The case of protonated water clusters in helium, J. Chem. Phys. 148, 102310 (2018)
[10] F. Brieuc, C. Schran, F. Uhl, H. Forbert, and D. Marx, Converged quantum simulations of reactive solutes in superfluid helium: The Bochum perspective, J. Chem. Phys. 152, 210901 (2020)
[11] R. Topolnicki, F. Brieuc, C. Schran, D. Marx, Deciphering High-order Structural Correlations within Fluxional Molecules from Classical and Quantum Configurational Entropy, J. Chem. Theory Comput. 16, 6785 (2020)
[12] L. Duran Caballero, C. Schran, F. Brieuc, and D. Marx, Neural network interaction potentials for para-hydrogen with flexible molecules, J. Chem. Phys. 157, 074302 (2022)
[13] R. Beckmann, F. Brieuc, C. Schran, and D. Marx, Infrared Spectra at Coupled Cluster Accuracy from Neural Network Representations, J. Chem. Theory Comput. 18}, 5492 (2022)
[14] H. R. Larsson, M. Schröder, R. Beckmann, F. Brieuc, C. Schran, D. Marx, and O. Vendrell, State-resolved infrared spectrum of the protonated water dimer: revisiting the characteristic proton transfer doublet peak, Chem. Sci. 13, 11119 (2022)
[15] J. Daru, H. Forbert, J. Behler, and D. Marx, Coupled Cluster Molecular Dynamics of Condensed Phase Systems Enabled by Machine Learning Potentials: Liquid Water Benchmark, Phys. Rev. Lett. 129, 226001 (2022); The PRL Editors: We have selected your recently accepted manuscript to be a PRL Editors' Suggestion. About one Letter in six is chosen for this highlighting. We look for papers that we judge to be particularly important, interesting, and well written.
Acknowledgement
It gives us great pleasure to thank Professor Jörg Behler for an enjoyable initial collaboration on his HD-NNP technique as well as for precious discussions while developing our implementation.
Bookmark
https://www.theochem.rub.de/go/RubNNet4MD.html
https://www.theochem.rub.de/go/rubnnet4md.html



